Summary of article (Van Rvenzwaaij)
The EZ diffusion model provides a powerful test of simple empirical effects
Van Rvenzwaaij, Donlin and Vandekerckhove
The diffusion model (Ratcliff 1978), or more specifically the drift diffusion model (DDM) is acknowledged as one of the leading models for understanding neural decision making. While the DMAT (see earlier review), one of the earlier ‘fitting models’, proposed by Vandekerckhove and Tuerlinckx (2008), was seen in these earlier years as a key model for fitting data to the diffusion model as proposed by Ratcliff (1978), it was a complex underlying model to address and the fitting model proved difficult to implement in practice (Vandekerckhove and Tuerlinckx [2008]).
It was for this reason that the EZ fitting model was proposed and developed. Wagenmakers, Van der Maas and Grasman (2007) developed the original model. The current authors undertake a study that undertake two separate evaluations, using the full diffusion model and compare the results with the E and TuerlinckxZ model.
The authors provide a good overview of the drift diffusion model with clear explanations of all of the various aspects of the model. The also include a very useful and clear graphic that provides better insight into the DMM and how it works. See Figure 1 below.
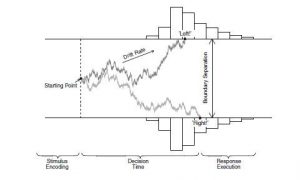
Figure 1: The Drift Diffusion Model
The authors then conducted four sets of simulations in two groups (full diffusion and EZ diffusion) based on Wagenmaker’s original data. They varied these simulations based on effects size (ranging from small SDs (0.5) to large SDs (1.2)), the number of participants ranging from10 to 50 in steps of 10, and the number of trials ranging from 50, through 100 to 200. They then performed t-tests on the difference between the drift parameters in each of the two groups (full diffusion model and EZ diffusion). They found that the EZ model is “a more powerful tool than the full diffusion model when attempting to detect a between-group effect on speed of information processing or response caution”.
Although they provide a comprehensive discussion of variability between these (and other) models, their conclusion is that “if researchers are interested in maximising the power of their design, analyzing their data with the full diffusion model is not always the best approach”. They argue that that “sometimes less is more” supporting the value and ease of the EZ model.
Reference:
Van Rvenzwaaij, D., Donlin, C. and Vandekerckhove, J. 2017. The EZ diffusion model provides a powerful test of simple empirical effects. Psychonomic Bulletin and Review, 24, pp. 547–556.